더보기
CS231n 강의 홈페이지: https://cs231n.stanford.edu/
CS231n Spring 2017 유튜브 강의 영상: https://www.youtube.com/watch?v=vT1JzLTH4G4&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk
강의 슬라이드 & 한글 자막: https://github.com/visionNoob/CS231N_17_KOR_SUB
Recap
- Loss Functions
- 함수 f는 입력 x에 따른 클래스들에 대한 스코어 벡터 Y를 출력
- 이에 대한 예측이 잘 된 혹은 잘 되지 않은 정도를 손실 함수를 통해 계산
- 손실 함수는 data loss term과 regularization term으로 구성
- 정규화 항은 모델의 복잡성을 조절함
- Optimization
- 최적의 파라미터 W를 찾는 과정
- 경사 하강법: 그래디언트의 반대 방향을 반복적으로 구해 가장 낮은 loss에 도달
- Numerical gradient: 유한 차분 근사(finite difference approximation)을 통해 계산. 매우 느리고 근사치임
- Analytic gradient: 미분을 통해 빠르고 정확하게 계산
Computational Graph

- Computational Graph를 사용하여 함수를 표현함으로써 backpropagation을 사용할 수 있음
- backpropagation은 그래디언트를 얻기 위해 Computational Graph 내부의 모든 변수에 대해 chain rule을 재귀적으로 사용
Backpropagation: a simple example

- \( x = -2, y = 5, z = -4 \)이고 \( f(x, y, z) = (x + y)z \)로 표현되는 함수가 있을 때 이를 computational graph로 표현하면 그림과 같다
- 구하고자 하는 것은 함수 \( f(x, y, z) \)의 출력에 대한 각 변수의 그래디언트인 \( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \)
- 이때 매개변수 \( q = x + y \)를 도입하여 \( f = qz \)로 표현
- 오류역전파는 재귀적인 방식이므로 뒤에서부터 값을 구해보면
- \( \frac{\partial f}{\partial z} = q = x + y = 3\)
- \( \frac{\partial f}{\partial y} = \frac{\partial f}{\partial q} \frac{\partial q}{\partial y} = z \times 1 = -4 \)
- \( \frac{\partial f}{\partial x} = \frac{\partial f}{\partial q} \frac{\partial q}{\partial x} = z \times 1 = -4 \)
- 그래디언트는 함수에 대한 각 변수의 영향력으로 해석할 수 있음
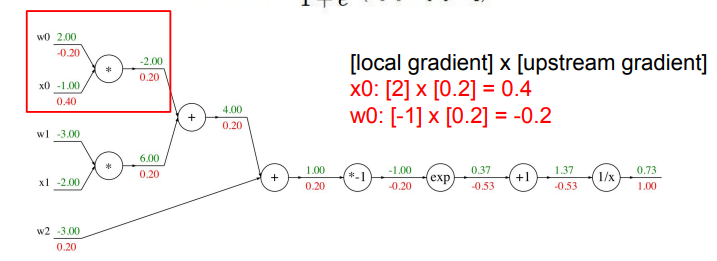
Local Gradient & Upstream Gradient

- 그래디언트를 구하기 위해 해당 노드와 바로 연결된 노드만 고려
- \( x, y \)에 대한 그래디언트를 구하기 위해 \( z \) 이외의 다른 부분은 고려하지 않음
- 그림에서와 같이 \( \frac{\partial L}{\partial x}, \frac{\partial L}{\partial y} \) 를 구하는 방법
- 'local gradient'인 \( \frac{\partial z}{\partial x}, \frac{\partial z}{\partial y} \)와
- 이전 단계에서 얻은 'upstream gradient'인 \( \frac{\partial L}{\partial z} \)를 각각 곱함
- 이러한 과정이 그래프의 앞단까지 반복적으로 진행됨
Backpropagation: another example

- 최종단의 upstream gradient를 1.00으로 가정. 계산 과정 ▼
- 나머지 단순 합노드와 곱노드 계산은 아래 그림과 같이 구함
- sigmode gate를 한 번에 계산
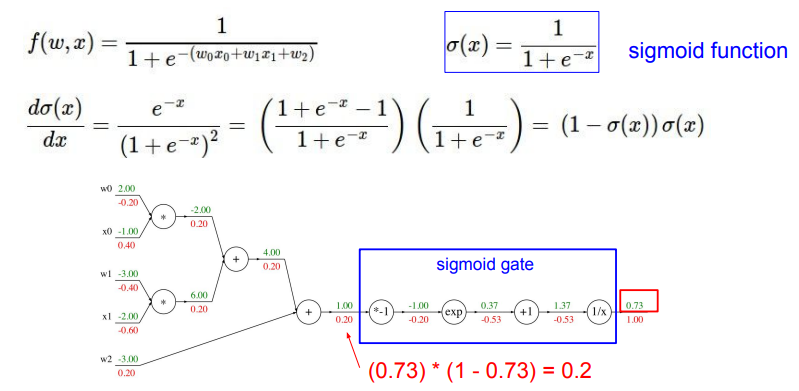
- \( \sigma (x) = \frac{1}{1+e^{-x}} \)일 때 \( \frac{\partial \sigma (x)}{\partial x} = (1 - \sigma (x))\sigma (x) \)임을 이용
- 그래프의 간결함 ↔ 계산의 복잡도는 trade-off 관계
Patterns in backward flow
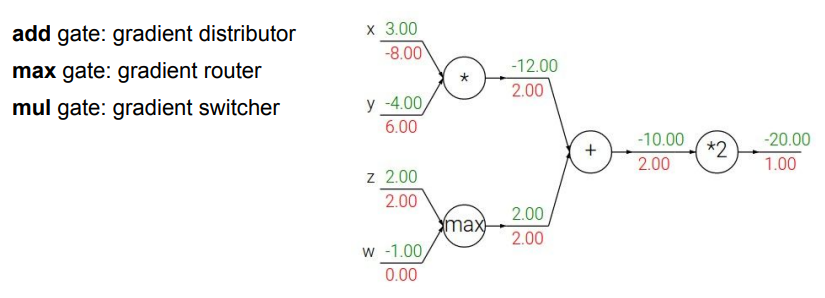
- add gate
- gradient distributor 역할
- local gradient의 값이 1이므로 upstream gradient의 값을 동일하게 분배해줌
- max gate
- gradient router 역할
- 최댓값이 전달된 노드로만 upstream gradient가 흐르게 해줌
- mul gate
- gradient switcher 역할
- 다른 변수의 값만큼 upstream gradient를 스케일링하여 전달해줌
Backpropagation with Vectors & Matrices


- 중요한 것은 원래 변수와 그래디언트의 차원이 동일해야 함 (차원분석을 통해 파악)
- 행렬곱 순서 유의: Downstream Gradient = Local Gradient * Upstream Gradient
- Example

Neural Networks

- 컴퓨팅 노드가 서로 연결되어 입력 신호를 받는 방식이 뉴런과 유사함
- 그러나 실제 생물학적 뉴런이 훨씬 복잡
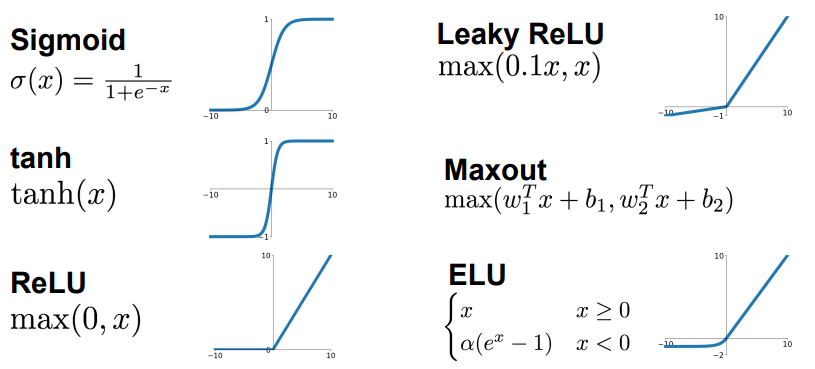
Activation Functions
Architectures of Neural Networks

- Fully-Connected layers (FC layers)
- FC layers는 각 레이어가 행렬 곱셈을 통해 연결됨
- 3-레이어 신경망은 2개의 히든 레이어로 구성
- 하나의 행렬 곱셈으로 여러 뉴런의 출력을 동시에 계산
- 비선형성을 적용하여 뉴런의 값을 계산하고 이를 다음 레이어로 전달
- Backpropagation
- 역전파 알고리즘을 통해 신경망의 가중치를 업데이트하여 학습을 진행
References
- 서울대학교 이준석 교수님 - 시각적 이해를 위한 머신러닝 (2023 spring)
- Lecture 4. Neural Networks & Backpropagation
- https://www.youtube.com/watch?v=KDmT15zv0Rc&list=PL0E_1UqNACXDTwuxUzCl5AeEjXBfWxCwc&index=4
'CS231n' 카테고리의 다른 글
| [CS231n] Lecture 7 | Training Neural Networks II (0) | 2024.08.13 |
|---|---|
| [CS231n] Lecture 6 | Training Neural Networks I (0) | 2024.08.08 |
| [CS231n] Lecture 5 | Convolutional Neural Networks (0) | 2024.07.30 |
| [CS231n] Lecture 3 | Loss Functions and Optimization (0) | 2024.07.26 |
| [CS231n] Lecture 2 | Image Classification (0) | 2024.07.24 |



