더보기
CS231n 강의 홈페이지: https://cs231n.stanford.edu/
CS231n Spring 2017 유튜브 강의 영상: https://www.youtube.com/watch?v=vT1JzLTH4G4&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk
강의 슬라이드 & 한글 자막: https://github.com/visionNoob/CS231N_17_KOR_SUB
Introduction to Loss Functions
- Recap of Linear Classifier
- 임의의 W 행렬을 사용하여 각 이미지에 대한 클래스 스코어를 계산
- 일부 스코어는 좋고 일부는 나쁨. 예를 들어, 고양이 이미지가 개구리보다 낮은 스코어를 받음
- 좋은 분류기란 올바른 클래스가 가장 높은 스코어를 받는 것
- Quantitattive Evaluation Method: Loss Function
- 스코어를 눈으로 보고 검사하는 것은 비효율적이며 주어진 W 행렬의 좋고 나쁨을 정량화하는 방법 필요
- 손실 함수는 W의 성능을 정량적으로 평가
- 가능한 모든 W 중에서 최적의 W를 찾는 과정을 최적화라고 함
Toy Example
간단한 3개의 클래스를 사용하는 toy 데이터셋을 사용한 예제

- Notations
- \( x \): 입력 이미지
- \( Y \) 레이블이나 타겟이라고 하며 CIFAR-10에서는 0에서 9 사이의 정수로 각 이미지의 정답 카테고리를 나타냄
- \( W \) : 가중치 행렬
- \( f(x, W) \): 입력 이미지 \( x \)와 행렬 \( W \)를 받아 \( Y \)를 예측하는 함수
- Defining the Loss Function \( L_{i} \)
- 예측 함수 \( f(x, W) \) 와 정답 값 \( Y \)를 입력으로 받아, 각 트레이닝 샘플을 얼마나 잘못 예측했는지를 정량화
- 전체 손실 \( L \)은 데이터 셋의 모든 샘플들의 손실 평균으로 정의
Multi-class SVM Loss Fuction
다중 클래스 SVM은 여러 클래스를 다루기 위해 이진 SVM을 일반화한 것

- Defining the Loss Function \( L_{i} \): Hinge loss
- \( max(0, s_{j} - s_{y_{i}} + 1) \)의 형태
- cat 클래스에 대한 손실을 구한다고 가정해보면 cat 클래스의 점수와 나머지 클래스 점수에 1을 더한 값을 비교
- 즉 cat score vs car score +1, cat score vs frog score +1 ...

- 즉 cat score vs car score +1, cat score vs frog score +1 ...
- 여기서 1은 safety margin
- 이 과정을 입력된 모든 샘플에 대해 진행
- 최종 손실은 모든 샘플의 손실에 대한 산술 평균

Final Loss
- 기하학적 해석

- 그래프의 모양 때문에 이러한 손실 함수를 hinge loss(경첩 손실)라고 부름
- x축은 실제 정답 클래스의 점수 \( s_{y_{i}} \)를 나타내고, y축은 손실을 나타냄
- 정답 클래스 점수가 높아질수록 손실이 선형적으로 줄어들며, 일정 마진을 넘어서면 손실은 0이 됨
- 정답 클래스의 점수가 나머지보다 margin 이상만큼 높을 수록 좋은 것으로 해석할 수 있음
- 1이라는 값은 점수들의 스케일링 정도에 따라 얼마든지 바뀔 수 있음. 중요한 것은 점수의 '차이'
Properties of SVM Loss
- Car 스코어가 조금 변하면 Loss는 어떻게 되는가?
- Car의 스코어를 조금 바꾸더라도 Loss가 바뀌지 않음
- SVM 손실 함수는 정답 스코어와 그 외의 스코어 간의 차이만 고려함. Car 스코어가 이미 다른 스코어들보다 매우 높다면, 스코어를 조금 바꾼다고 해도 margin이 여전히 유지되므로 Loss는 변하지 않고 계속 0일 것임
- SVM Loss가 가질 수 있는 최댓값과 최솟값
- 정답 클래스의 스코어가 가장 클 때 모든 샘플에서 Loss가 0이 되기 때문에 최솟값은 0
- 정답 클래스 스코어가 매우 낮은 음수 값을 가질 때 Loss는 무한대가 될 수 있음
- 그래프를 보면 알 수 있음
- 처음 학습 시 행렬 W를 임의의 작은 수로 초기화시켰을 때 결과 스코어가 거의 0에 가깝고 값이 비슷하다면 Loss는 어떻게 되는가?
- Loss 값은 클래스의 수 - 1이 됨
- 정답이 아닌 클래스를 순회하며 비교하는 두 스코어가 거의 비슷하기 때문에, 1의 스코어를 얻게 되고(margin) 따라서 Loss는 클래스의 수 - 1이 됨. 이를 디버깅 전략으로도 활용할 수 있음
- 정답 클래스도 포함해 모든 스코어를 다 더한다면?
- Loss 값 1 증가
- 자기 자신 - 자기 자신 + 1 = 1이기 때문. 그러나 Loss를 0으로 맞추는 것이 이상적이기 때문에 일반적으로는 사용하지 않음
- Loss에서 전체 합을 쓰는 대신 평균을 쓴다면?
- 클래스의 수는 정해져 있으므로 평균을 취하는 것은 단순히 손실 함수를 리스케일할 뿐임. 따라서 큰 차이가 없음
- 손실 함수를 제곱 항으로 바꾸면 결과가 달라지는가?
- 제곱 항을 사용하면 손실 함수의 계산 방식이 비선형적으로 바뀌며, '좋은 것과 나쁜 것' 사이의 트레이드 오프가 달라짐
- '나쁜 것'의 패널티를 더 크게 부여
Multi-class SVM Loss: Example code

- numpy를 통한 vectorized
- margin[y] = 0 부분은 정답 클래스를 0으로 바꿔주는 것
Which W should we choose?
- 손실 함수와 가중치

- 손실 함수가 0이 되게 하는 W 값은 하나가 아닐 수 있음
- W의 스케일을 두 배로 늘려도 손실 함수 값은 변하지 않을 수 있음
- Overfitting

- 모델은 훈련 데이터가 아닌 새로운 데이터에 대한 성능이 높아야 함
- 훈련 데이터에 지나치게 맞추면, 새로운 데이터(테스트 데이터)에는 잘 맞지 않는 과적합(overfitting) 문제가 발생할 수 있음
- 그림의 훈련 데이터(파란 점)를 잘 예측할 뿐만 아니라 새로운 데이터(초록 네모)도 잘 예측할 수 있도록 해야함
- Regularization (정규화)

- 정규화는 모델이 너무 복잡해지는 것을 막기 위해 손실 함수에 추가되는 항
- 오컴의 면도날
- 다양한 가설이 동일한 현상을 설명할 수 있다면 일반적으로 더 단순한 가설을 선호
- 더 단순하 가설이 미래의 현상을 설명할 가능성이 더 높기 때문
- 정규화 항은 모델이 좀 더 단순한 W 값을 선택하도록 도와줌
- 최종적으로 손실 함수는 Data loss term과 Regularization term으로 구성
- 정규화의 하이퍼파라미터 lambda는 data loss term과 regularization term 간의 균형을 조절
Various Regularization Methods

- L2 Regularization (Weight Decay)
- 가장 보편적인 정규화 기법
- 가중치 행렬 W에 대한 L2 norm 또는 squared norm
- W의 norm을 작게, 즉 더 coarse하게 만듦 (x의 모든 요소가 영향을 주도록)
- L1 Regularization
- 가중치 행렬 W에 대한 L1 norm
- W의 요소들이 0이 되게(희소행렬), 즉 더 sparse하게 만듦
- Elastic Net Regularization
- L1과 L2 정규화를 혼합한 방식
- Max Norm Regularization
- L1, L2 대신 max norm을 사용하는 방식
- Example

- 선형 분류 관점에서 w1과 w2는 동일 (내적 값 동일)
- L2 Regularization은 norm이 더 작은 w2를 선호
- L1 Regularization은 더 sparse한 w1을 선호 선택
- 어떤 정규화를 사용할지 선택하는 것은 '복잡하다'라는 것을 어떻게 정의하는지에 따라 달라짐
Cross-entropy Loss
- 앞서 Multi-class SVM loss에서는 정답 클래스 스코어와 나머지 클래스 스코어의 차이만을 고려할 뿐 스코어 자체에 대한 해석은 고려하지 않았음
- Multinomial Logistic Regression(Softmax Classifier)의 손실 함수는 스코어 자체에 추가적인 의미를 부여

- Defining the Loss Function \( L_{i} \)
- \( -log(\frac{e^{s_{y_{i}}}}{\sum_{j} e^{s_{j}}}) \)의 형태 ▶ -log(확률)
- 각 클래스에 대한 스코어를 지수화하여 확률로 변환
- 계산된 확률 분포는 각 클래스에 대한 확률을 나타내며, 모든 확률의 합은 1이 됨
- 해석
- 최솟값과 최댓값
- 최솟값은 0, 최댓값은 무한대
- 이는 이론상의 값일 뿐 유한 정밀도로 인해 도달할 수는 없음
- 모든 스코어가 0에 가깝게 모여있다면?
- Loss 값은 \( -log(\frac{1}{c})=log(c) \)가 됨
- 최솟값과 최댓값
SVM Loss vs. Softmax Loss


- SVM Loss
- 스코어 해석 없음: 스코어 자체에 의미를 부여하지 않으며, 단지 정답 클래스의 스코어가 다른 클래스의 스코어보다 높기만을 요구
- 스코어 간의 차이를 중심으로 손실을 계산
- margin을 넘기만 하면 성능 개선이 이루어지지 않음
- Softmax Loss
- 스코어 해석: 각 클래스의 스코어가 해당 클래스에 속할 확률로 해석됨
- 확률 분포를 사용하여 손실을 계산
- 정답 클래스의 확률을 최대화하도록 지속적인 성능 개선이 이루어짐
Optimization
- 손실 함수를 최소화하기 위해 파라미터 W를 찾는 과정을 최적화라고 함
- 이 과정은 마치 우리가 큰 협곡을 걷는 것과 비슷하게 상상할 수 있음. 파라미터 W는 협곡의 지형이고, 높이는 손실을 나타냄. 우리의 목표는 협곡의 밑바닥, 즉 최소 손실을 찾는 것
- 기본적인 방법: Random Search
- 가장 단순한 최적화 기법으로서 다양한 W값을 임의로 선택하고 각각의 손실을 계산하여 가장 낮은 손실을 주는 W를 선택하는 방법
- 매우 비효율적
- 기하학적 특징을 이용한 더 나은 방법: Gradient Descent
- 협곡을 걸을 때, 우리는 눈으로 밑바닥을 보지 못하더라도 발로 느껴서 경사를 파악할 수 있음. 이러한 방법을 사용하면 결국 계곡의 밑바닥에 도달할 수 있음
- 경사하강법은 가장 많이 사용되는 최적화 방법 중 하나로, 이 방법에서는 손실 함수의 기울기(경사)를 계산하여 손실을 줄이는 방향으로 파라미터 W를 업데이트함
- 경사 (Gradient): 1차원 함수에서 경사는 미분값. 예를 들어, 함수 f(x)에서 x의 경사는 \( \frac{df}{dx} \)로 표현됨
- 다변수 함수: 다변수 함수에서는 벡터 의 각 요소에 대한 편미분값을 모은 벡터인 그래디언트(Gradient)로 확장됨. \( \nabla f \)로 표현되는 그래디언트는 함수의 증가 방향을 나타냄
- gradient의 반대 방향은 곧 가장 많이 내려갈 수 있는 방향
Computing Gradient Descent
- Finite Different Method (유한 차분법)

- 현재 파라미터 W로 손실 함수 L(W)계산
- W의 첫 번째 요소 w1에 아주 작은 값 h를 더한 새로운 파라미터 W'로 손실 함수 L(W')를 다시 계산함
- 그림과 같이 L(W), L(W')를 이용하여 그래디언트를 구함
- 첫 번째 요소뿐만 아니라 모든 요소에 대해서도 반복
- 매우 비효율적이지만 디버깅 전략으로 활용할 수 있음
- Analytic Method

- 미분을 통해 한 번의 계산으로 정확하고 빠르게 그래디언트를 얻을 수 있음
Gradient Descent: Example Code

- W를 임의의 값으로 초기화
- Loss와 gradient를 계산한 뒤에 가중치를 gradient의 반대 방향으로 업데이트
- step size는 learning rate라고도 하며 실제 학습시 가장 중요하고 우선적으로 정해줘야 할 하이퍼파라미터
Stochastic Gradient Descent (SGD)

- 트레이닝 샘플의 개수가 매우 많다면, 즉 N이 크다면 이에 대한 Loss와 gradient를 계산하는 것은 매우 오래 걸리는 작업
- SGD는 미니배치라고 하는 작은 집합들로 전체 데이터를 분할하여 경사 하강법을 수행
- 미니배치 크기는 보통 32, 64, 128 등과 같이 2의 n제곱수로 정함
Image Features

- 이미지의 픽셀을 직접 사용하는 방법은 Multi-Modality 문제 등으로 인해 성능이 좋지 않음
- DNN이 등장하기 전에는 이미지를 직접 입력으로 사용하는 대신, 두 단계로 이루어진 방법을 사용함
- 이미지에서 다양한 특징을 계산
- 계산된 특징들을 하나의 벡터로 결합하여(concat) Linear Classifier의 입력으로 사용
Examples
- 컬러 히스토그램

- 이미지의 색상을 기반으로 한 간단한 특징 벡터
- 각 픽셀의 색상 정보를 수집하여 색상 히스토그램을 생성
- Histogram of Oriented Gradients (HOG)

- 이미지의 로컬 영역에서 지배적인 엣지 방향을 계산하여 히스토그램을 만드는 방법
- 8x8 픽셀 블록: 이미지를 8x8 블록으로 나누고, 각 블록 내에서 주요 엣지 방향을 계산
- 히스토그램 계산: 엣지 방향을 양자화하여 히스토그램으로 표현하고, 이를 특징 벡터로 사용
- 예를 들어 그림에서 HOG는 대각선 엣지를 많이 포함한 이파리를 정확하게 특징으로 잡아냅니다.
- Bag of Words (BOW)
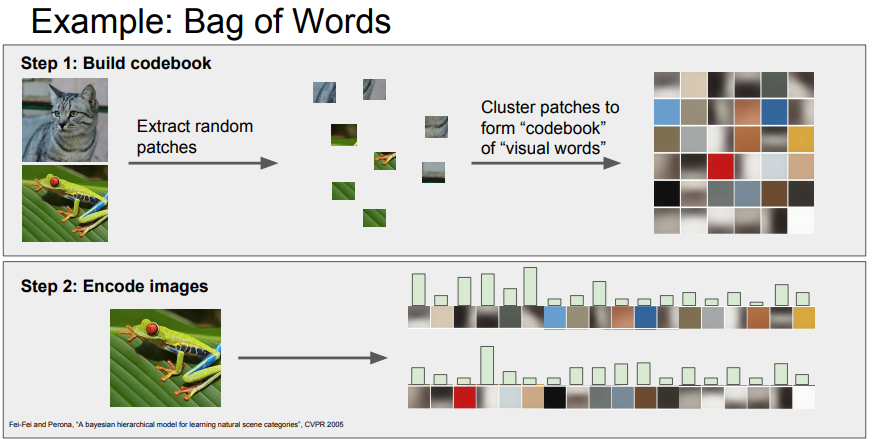
- 자연어 처리에서 영감을 받은 방법
- 이미지를 임의로 조각낸 다양한 패치를 K-means 알고리즘으로 군집화하여 '시각 단어(visual words)'를 만듦
- 시각 단어들이 모여 '코드북(codebook)'을 형성
- 새로운 이미지에서 시각 단어의 발생 빈도를 계산하여 이미지 특징 벡터를 만들 수 있음
'CS231n' 카테고리의 다른 글
| [CS231n] Lecture 7 | Training Neural Networks II (0) | 2024.08.13 |
|---|---|
| [CS231n] Lecture 6 | Training Neural Networks I (0) | 2024.08.08 |
| [CS231n] Lecture 5 | Convolutional Neural Networks (0) | 2024.07.30 |
| [CS231n] Lecture 4 | Introduction to Neural Networks (0) | 2024.07.29 |
| [CS231n] Lecture 2 | Image Classification (0) | 2024.07.24 |