더보기
CS231n 강의 홈페이지: https://cs231n.stanford.edu/
CS231n Spring 2017 유튜브 강의 영상: https://www.youtube.com/watch?v=vT1JzLTH4G4&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk
강의 슬라이드 & 한글 자막: https://github.com/visionNoob/CS231N_17_KOR_SUB
Overview of Recurrent Neural Networks
- Vanilla Neural Networks
- 지금까지 살펴본 아키텍처들은 고정된 길이의 이미지 또는 벡터를 입력으로 받아 하나의 출력을 내보냄
- 이는 다양한 길이의 입력 및 출력을 다루기 어렵다는 한계가 존재
- RNN을 사용한 다양한 입출력 모델

- RNN은 다양한 형태의 입력과 출력 처리에 용이함
- One to Many
- e.g. Image Captioning
- 이미지 → 캡션
- Many to One
- e.g. Sentiment Classification
- 문장 → 감정 분석
- Many to Many
- e.g. Machine Translation
- 문장 → 번역
- Many to Many
- e.g. Video classification on frame level
- 비디오 프레임 → 분류
- 장점
- RNN은 입력과 출력의 길이가 다양할 수 있는 데이터를 처리하는 데 최적화되어 있음
- 고정된 입출력이라도 sequential processing이 필요한 경우 유용하게 사용됨
- 예를 들어 이미지의 여러 부분을 순차적으로 살펴보고 분류하거나 이미지를 순차적으로 생성해낼 수 있음
Recurrent Neural Network
- Basics
- RNN은 작은 Recurrent Core Cell을 가지고 있음
- 입력 x가 들어올 때마다 내부의 hidden state가 업데이트되어 이 정보가 반복적으로 사용됨
- Recurrence formula

- RNN block은 함수 \( f \)로 나타낼 수 있고 파라미터 \( W \)를 가짐
- 함수 \( f \)는 이전 단계의 hidden state \( h_{t-1} \)와 현재 입력 \( x_t \)를 받아 새로운 hidden state \( h_t \)를 계산
- 중요한 점은 함수 \( f \)와 파라미터 \( W \)는 모든 단계에서 동일
- Details

- 더 구체적으로는 그림과 같이 가중치 행렬의 곱과 tanh을 통해 hidden state를 얻음
- 출력 값 \( y_t \)를 얻기 위해 FC layer를 추가하여 매번 업데이트된 hidden state \( h_t \)를 입력으로 받아 출력을 결정할 수 있음
RNN: Computational Graph
- Unrolling RNN

- 그림과 같이 RNN을 unrolling하면 time step마다 변화하는 hidden state, 입/출력, 가중치 간의 관계를 더 명확히 이해할 수 있음
- 각 time step에서 이전 hidden state \( h_0 \)와 입력 \( x_t \)가 함수 \( f_w \)에 들어가 다음 hidden state \( h_1 \)가 출력됨. 이 과정은 반복되며 다음 입력 \( x_2 \)가 들어옴
- 첫 step에서의 initial hidden state \( h_0 \)는 보통 0으로 초기화됨
- 중요한 점은 모든 step에서 동일한 가중치 행렬 \( W \)가 사용된다는 것
- Backpropagation
- 만약 각 time step에서의 출력 \( y_t \)가 개별적으로 존재한다면 각각의 \( y_t \)에 대한 loss를 개별적으로 계산할 수 있음
- 이를 바탕으로 각 time step에서 가중치 \( W \)에 대한 로컬 그래디언트를 계산한 뒤 이를 모두 더해 최종 그래디언트를 구함
- Many to Many

- Many to One

- 감정 분석과 같은 many to one 구조에서는 최종 hidden state에서만 결과가 나옴. 이는 전체 시퀀스를 요약하는 역할을 함.
- One to Many

- 고정된 입력을 받지만 가변적인 출력을 내는 구조. 이 경우 고정 입력은 대개 initial hidden state를 초기화하는 용도로 사용되고, 이후 모든 step에서 출력이 생성됨.
Sequence to Sequence: Many to one + One to many
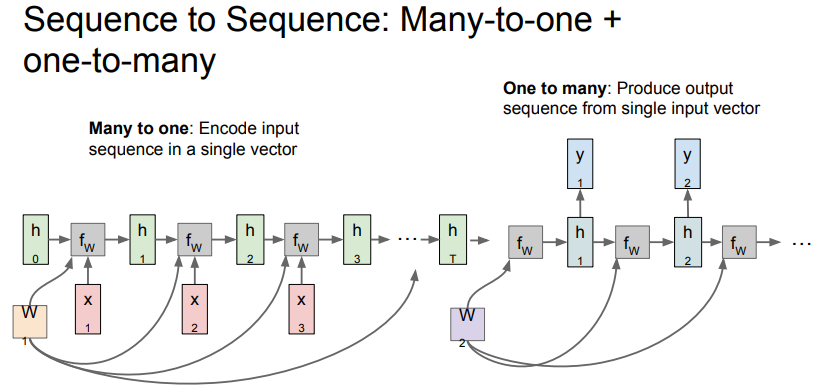
- machine translation에 사용할 수 있는 구조
- many to one과 one to many 구조가 결합된 형태로 가변 입력과 가변 출력을 가짐
- Encoder
- many to one 구조
- 문장과 같은 가변 입력을 받아 final hidden state를 통해 전체 문장을 하나의 벡터로 요약
- Decoder
- one to many 구조
- 앞서 요약한 하나의 벡터를 입력으로 받아 매 step마다 적절한 단어를 출력
Example: Character-level Language Model
- Language Modeling
- RNN은 자연어 처리에서 자주 사용되며 특히 언어 모델링에 유용
- 언어 모델링은 주어진 문맥에서 다음 단어나 문자를 예측하는 문제
- Character-Level Language Model 예제
- 모델이 "hello"라는 단어를 학습하는 예제
- Vocabulary는 [h, e, l, o]로 구성
- 각 문자는 one hot 벡터로 표현. 예를 들어 'h'는 [1, 0, 0, 0]
- 모델은 각 스텝에서 다음 문자를 예측
- Train Time

- 모델은 입력 \( x_t \)에 대한 다음 문자 \( y_t \)를 예측
- 첫 예측에서 모델은 입력 문자 'h'에 대해 다음 문자를 'e' 대신 'o'로 잘못 예측함. 이 결과가 softmax loss에 반영됨
- 이어서 다음 입력 'e'에 대해 이전 hidden state와 함께 새로운 hidden state를 만들어냄. 마찬가지로 'l' 대신 'o'로 잘못 예측하여 loss에 반영
- 이 과정이 반복됨
- Test Time

- Test time에서 모델은 학습한 내용을 바탕으로 Sampling을 통해 문장을 생성
- 예를 들어 'h'가 입력된다면 모델은 기존 vocabulary를 바탕으로 모든 문자에 대한 스코어(확률)를 얻을 수 있음
- 예제의 경우 'e'의 확률이 낮음에도 불구하고 샘플링을 통해 'e'가 선택되었고 이제 'e'가 다음 스텝의 입력으로 들어감
- 이 과정이 반복됨
- 가장 높은 스코어를 선택하는 것이 아닌 샘플링을 하는 이유는 모델의 다양성을 확보하기 위함 (안정성-다양성 trade off 관계)
- Truncated Backpropagation

- 앞서 RNN에서는 각 스텝에서의 출력값의 loss를 합산해 최종 loss를 계산하고 이를 바탕으로 역전파를 수행한다고 하였음
- 그러나 이는 시퀀스가 길어질수록 메모리 사용량과 계산 시간이 증가한다는 단점이 존재
- 이를 해결하고자 긴 시퀀스를 다룰 때는 Truncated Backpropagation을 사용해 일정한 길이(e.g. 100 스텝)로 나눈 서브시퀀스만을 가지고 loss를 계산하고 그때마다 gradient를 업데이트함
- 이때 이전 배치에서 계산된 hidden state는 그대로 유지하여 다음 배치에서 사용
- 쉽게 말해 시퀀스 데이터에서의 Stochastic Gradient Descent 방식
RNN in Image Captioning
- Idea
- RNN과 CNN을 결합하여 이미지 정보를 바탕으로 캡션을 생성
- 지도 학습 방법으로 학습되며 COCO와 같이 natural language caption이 존재하는 이미지 데이터셋이 필요함
- Details


- CNN: 입력 이미지에서 요약된 이미지 정보를 포함한 벡터를 출력
- RNN: CNN으로부터 추출된 벡터와 <START> 토큰을 를 초기 입력으로 받아 단어를 반복적으로 샘플링하며 캡션 생성
- 이미지 벡터라는 새로운 입력이 추가되었으므로 \( W_ih \)라는 가중치가 cell에 새롭게 추가됨
- 시퀀스의 끝을 나타내는 <END> 토큰을 포함하여 학습
- Results


Good & Bad results - 훈련 데이터와 유사한 이미지에 대해서는 매우 그럴 듯한 캡션을 만들어냄
- 새로운 유형의 이미지나 일반화된 문제를 푸는 데에는 한계가 있음
Image Captioning with Attention
- Idea
- 이미지의 특정 부분에 집중(attention)하여 캡션을 생성하는 모델.
- CNN을 통해 이미지의 다양한 위치 정보를 포함한 벡터들을 생성하고 RNN은 각 위치에 대한 attention을 통해 캡션을 생성
- Details

- CNN은 이미지로부터 특징 벡터(LxD) 출력
- RNN은 vocabulary에 대한 분포(d) 뿐만 아니라 이미지를 집중해서 볼 위치에 대한 분포(a)도 생성
- 그림과 같이 첫 번째 hidden state에서는 이미지의 위치에 대한 분포(a1)만을 생성하고 이를 이미지 특징 벡터와 계산하여 요약된 벡터(z1)를 생성. z1은 다시 다음 스텝의 입력으로 사용
- 이 과정을 반복하며 매 스텝에서 두 개의 분포(a, d)를 생성
- Soft & Hard Attention

- Soft Attention: 모든 이미지 위치와 모든 특징 간의 weighted combination을 취함
- Hard Attention: 한 번에 한 곳만 집중하게 강제하는 방식. 학습 시 강화 학습을 사용해야 함
Multilayer RNNs

- 앞서는 hidden state가 하나뿐인 단일 레이어 RNN을 다뤘지만 멀티 레이어 RNN이 더 흔하게 사용됨
- 그림과 같은 3-layer RNN을 예로 들면 입력이 첫 번째 레이어 RNN으로 들어가서 hidden state의 시퀀스를 만듦
- 이 시퀀스를 다시 입력으로 넣어 두 번째 레이어가 또 다른 hidden state의 시퀀스를 만듦
- 일반적으로 RNN에서는 3~4개 정도의 레이어를 사용
Gradient Flow in Vanilla RNN
- Recap

- 바닐라 RNN의 작동 원리를 되짚어보면 입력은 현재 입력 \( x_t \)와 "이전 hidden state \( h_{t-1} \)로 이루어짐
- 이 두 입력을 쌓아서 가중치 행렬 \( 와 행렬 곱 연산을 수행하고 함수를 적용하여 다음 hidden state \( h_t \)를 만듦
- Problems in Backpropagation

- Backward pass시에는 \( h_t \)에 대한 loss의 미분값을 계산하여 이를 이전 hidden state \( h_{t-1} \)로 전파함
- 이 과정에서 각 RNN cell을 거칠 때마다 가중치 행렬의 전치 행렬을 곱하게 됨
- 그러나 이 곱연산은 수백 ~ 수천 개의 스텝이 있는 경우라면 그래디언트가 지나치게 커지거나 작아지는 문제가 발생할 수 있음
- Exploding Gradient
- 각 시퀀스의 cell을 통과할 때 가중치 행렬의 특이값(singular value)이 1보다 크면 그래디언트가 점점 커져서 기하급수적으로 증가
- 이로 인해 그래디언트 폭발 문제가 발생
- Vanishing Gradient
- 반대로 가중치 행렬의 특이값이 1보다 작은 경우 그래디언트가 점점 작아지면서 0에 가까워짐
- 이로 인해 학습이 거의 이루어지지 않는 그래디언트 소멸 문제가 발생
- Gradient Clipping
- 그래디언트 폭발 문제를 완화하기 위해 사용하는 휴리스틱 방법
- 그래디언트의 L2 norm이 특정 임계값을 넘지 못하도록 제한하여 기하급수적으로 커지는 것을 방지
- 그러나 이 방법은 그래디언트 소멸 문제를 해결하지는 못함
Long Short Term Memory (LSTM)
Idea
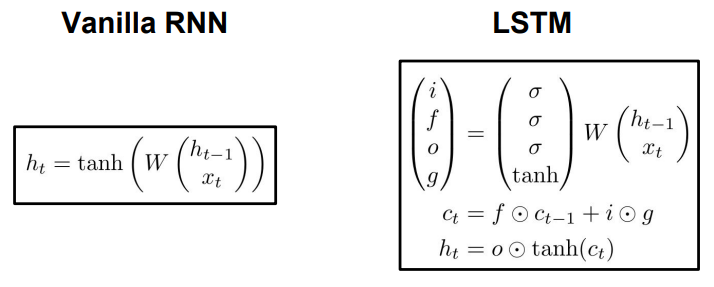
- 1997년에 공개되어 RNN의 그래디언트 폭발, 소멸 문제를 완화하기 위해 사용됨
- Gradient Clipping 같은 방법을 사용하지 않고 아키텍처 자체에서 그래디언트가 잘 전달되도록 디자인
- 두 개의 hidden state \( h_t \)와 \( c_t\ )를 가짐
- \( h_t \): RNN의 hidden state와 유사
- \( c_t \): cell state로 LSTM 내부에서만 존재. 외부에 노출되지 않음
Details
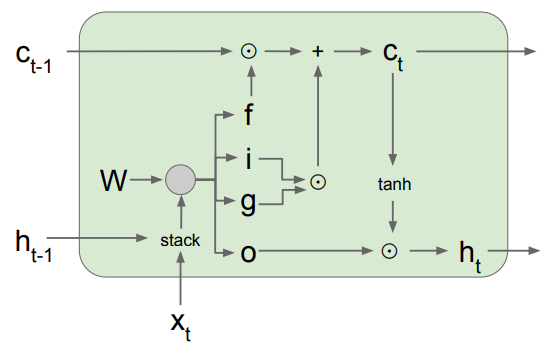
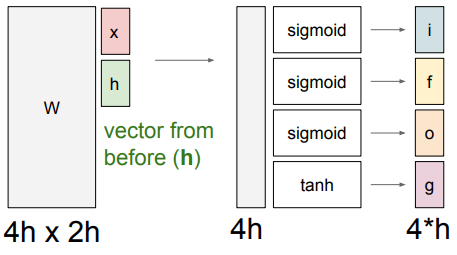
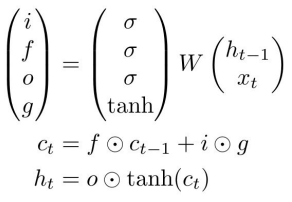
- LSTM도 마찬가지로 \( h_{t-1} \)과 현재 입력 \( x_t \)을 받음
- 차이점은 추가적인 4개의 게이트가 존재하는데 이들은 내부에서 \( c_t \)를 계산하는 데에 사용되고 계산된 \( c_t \)는 \( h_t \)를 만드는 데에 사용됨
- Forget Gate (f)
- 시그모이드 게이트로서 0 ~ 1의 값
- 이전 스텝의 \( c_{t-1} \)와 element-wise 곱셈을 수행하여 이전 cell state의 정보를 얼마나 망각할지 결정 (0이면 잊고 1이면 기억)
- Input Gate (i)
- 시그모이드 게이트로서 0 ~ 1의 값
- 현재 \( c_t \)에 대해 새로운 정보를 사용할지를 결정
- Gate Gate (g)
- tanh 게이트로서 -1 ~ 1의 값
- 현재 \( c_t \)에 대해 새로운 정보를 얼마나 사용할지를 결정
- Output Gate (o)
- 시그모이드 게이트로서 0 ~ 1의 값
- 현재 \( c_t \)를 얼마나 노출시킬지를 결정
Gradient Flow
- Backpropagation

- \( c_t \)에서 \( c_{t-1} \)로 그래디언트가 흐르는 과정을 살펴보면 가장 먼저 addition operation을 만나는데 이때는 단순히 upstream gradient가 두 갈래로 복사됨
- 따라서 최종 그래디언트는 upstream gradient ⊙ forget gate 라고 할 수 있음
- 장점

- 행렬곱이 아닌 element-wise 곱 (행렬곱으로 얽히지 않고 독립적으로 계산)
- 매 스텝마다 달라지는 forget gate 값 (0~1의 값으로 수치적 안정성 + 정보의 유지/망각 용이)
- tanh를 한 번만 거치면 됨
- 이러한 이유로 최종 loss부터 초기 cell state까지 그래언트가 비교적 원활하게 흐를 수 있으며 그래디언트 소멸, 폭발 문제를 완화할 수 있음
'CS231n' 카테고리의 다른 글
| [CS231n] Lecture 9 | CNN Architectures (0) | 2024.08.26 |
|---|---|
| [CS231n] Lecture 8 | Deep Learning Software (0) | 2024.08.19 |
| [CS231n] Lecture 7 | Training Neural Networks II (0) | 2024.08.13 |
| [CS231n] Lecture 6 | Training Neural Networks I (0) | 2024.08.08 |
| [CS231n] Lecture 5 | Convolutional Neural Networks (0) | 2024.07.30 |